Réseaux de Bravais : Différence entre versions
| Ligne 1 : | Ligne 1 : | ||
En cristallographie, les réseaux de bravais représentent une façon mathématique (géométrie dans l'espace) de classifier les différents types de cristaux. | En cristallographie, les réseaux de bravais représentent une façon mathématique (géométrie dans l'espace) de classifier les différents types de cristaux. | ||
| + | voici les différents systèmes: | ||
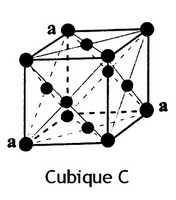
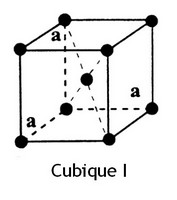
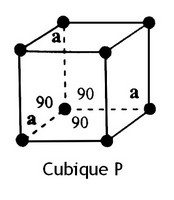
| − | + | Systèmes Cubiques (F, I et P) | |
[[Image: Cubique F.jpg]] | [[Image: Cubique F.jpg]] | ||
| Ligne 8 : | Ligne 9 : | ||
[[Image: Cubique P.jpg]] | [[Image: Cubique P.jpg]] | ||
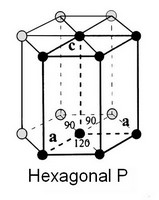
| − | + | Systèmes hexagonal (P) | |
[[Image:Hexagonal P.jpg]] | [[Image:Hexagonal P.jpg]] | ||
| Ligne 24 : | Ligne 25 : | ||
[[Image:Orthorhombique P.jpg]] | [[Image:Orthorhombique P.jpg]] | ||
| − | Système | + | Système Tétragonaux (I et P) |
| − | [[Image: | + | [[Image:Tetragonaux I.jpg]] |
| − | [[Image: | + | [[Image:Tetragonaux P.jpg]] |
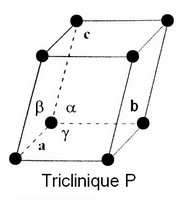
Système Triclinique (P) | Système Triclinique (P) | ||
Version du 18 janvier 2009 à 21:31
En cristallographie, les réseaux de bravais représentent une façon mathématique (géométrie dans l'espace) de classifier les différents types de cristaux.
voici les différents systèmes:
Systèmes Cubiques (F, I et P)
Systèmes hexagonal (P)
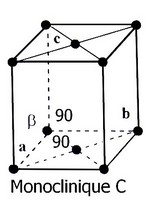
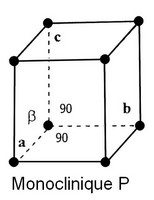
Système Monoclinique (C et P)
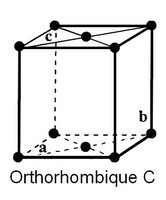
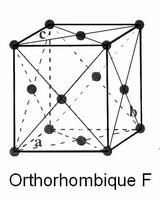
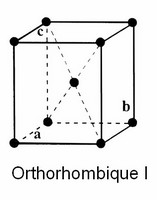
Système Orthorhombique (C, F, I et P)
Système Tétragonaux (I et P)
Fichier:Tetragonaux I.jpg Fichier:Tetragonaux P.jpg
Système Triclinique (P)
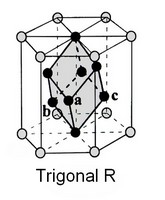
Système Trigonal (R)