Compléments sur la dureté, la densité et l'indice de réfraction

Origine physicochimique de l'indice de réfraction

et de la dureté des minéraux

Introduction

Dans la partie détermination des minéraux est proposée une approche descriptive des concepts de densité et de dureté et de l'indice de réfraction (par intermédiaire de l'éclat des minéraux). Le but étant de fournir les outils nécessaires à la détermination des minéraux, l'origine physicochimique n'en est pas abordée. Cet article propose de lever le voile sur l'origine de la dureté et de l'indice de réfraction et de regarder les relations qui peuvent exister entre dureté, densité et indice de réfraction.

Plus de détails sur l’indice de réfraction

Une façon de juger qualitativement de l'indice de réfraction d'un minéral est d'observer son éclat. Plus l'éclat tendra vers l'adamantin et plus l'indice de réfraction sera important. D'après la loi de Gladstone-Dale, il y a une dépendance linéaire entre l'indice de réfraction et la densité : plus la densité est élevée et plus l’indice de réfraction est important. Cette loi n'est valable en toute rigueur que pour les gaz, mais est très bien respectée pour les polymorphes du quartz. Cette loi stipule qu'à composition chimique égale plus un produit sera dense et plus son indice de réfraction sera important c'est-à-dire que l'éclat tendra vers l'adamantin. L’évolution de l’indice de réfraction en fonction de la densité pour les polymorphes du quartz est présentée ci-dessous.

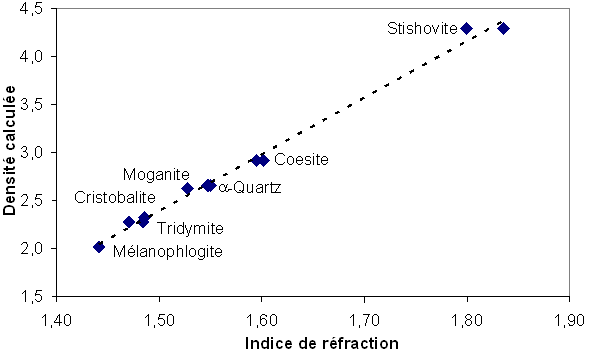
L'indice de réfraction de la grande majorité des minéraux, ne dépend que de la "permittivité électrique" du matériau par la relation avec n l’indice de réfraction et la permittivité électrique. La notion de permittivité électrique est facilement explicable, pour cela nous devons nous intéresser à la lumière. La lumière est une onde électromagnétique, elle transporte donc une information électrique et magnétique. Pour notre raisonnement il est utile de souligner que les atomes possèdent tous des électrons qui sont des charges et sont donc sensibles aux champs électriques. Ainsi on peut donner un sens à la permittivité électrique qui traduit la facilité de déformer le nuage d'électrons qui gravitent autour de l'atome, on parle aussi d’orbitale atomique. Plus ce nuage est déformable, plus la permittivité est grande et plus l'indice de réfraction est grand. Un atome dont le nuage électronique se déforme sous l'action d'un champ électrique est dit polarisable. Plus un atome sera gros et plus ses orbitales seront diffuses, c'est-à-dire que les électrons seront très éloignés du noyau de l’atome. Ainsi ils seront moins influencés par l’action attractive du noyau (les charges + attirent les charges –) et donc plus sensibles aux champs électriques externes. Plus un atome sera gros et plus il sera polarisable. C’est le cas du cadmium, du plomb et du bismuth, mais il en existe beaucoup d’autres. Les atomes polarisables du tableau périodique des éléments sont généralement associés à une importante densité. Cette loi n’est pas générale : une densité importante n’est pas fondamentalement associée à un indice de réfraction important. Nous le verrons plus en détail par la suite.
Nous avons vu que l’indice de réfraction dépend de la polarisabilité des atomes. Or dans le cas des polymorphes de la silice, l’indice de réfraction évolue alors que la composition reste la même. Pour comprendre ce phénomène il faut s’intéresser au concept de liaison chimique, ce qui renvoie à la notion de dureté.

Plus de détails sur la dureté : Le concept de liaison chimique

La dureté est une affaire de liaisons chimiques. Pour un solide isotrope (système cubique) plus les liaisons entre atomes seront covalentes et plus le solide sera dur. Par exemple un solide presque totalement ionique comme l'halite est très peu dur alors que le diamant qui est un composé extrêmement covalent (on ne peut pas faire mieux à vrai dire) est le plus dur tous. Ces deux liaisons sont totalement distinctes au niveau des mécanismes électroniques qui leur donnent naissance. Dans le cas de la liaison covalente, c’est un partage équitable des électrons entre les atomes qui assure le lien entre atomes. On parle alors ici de délocalisation des électrons. Pour la liaison ionique c’est une interaction électrostatique attractive entre un cation et un anion : les charges + (cations) sont attirées par les charges – (anions). On parle alors de liaison polaire ou de polarisation car tous les électrons sont coincés au niveau des anions et ne se délocalisent pas au niveau des cations.
Dans la nature les choses ne sont pas aussi tranchées. La plupart des composés présentent des liaisons qui sont intermédiaires entre la liaison ionique et la liaison covalente. En effet il y a toujours un mélange entre délocalisation des électrons (covalence) et polarisation de la liaison (ionicité). On parle alors de ionocovalence de liaison. Schématiquement les électrons vont accepter de se délocaliser sur l’ensemble de la liaison, mais ils préféreront rester un peu plus au voisinage des anions.
Dans les solides non isotropes, les choses se compliquent au niveau de la dureté car suivant les plans cristallins, les liaisons n'ont pas le même caractère ionique et covalent. Cela explique que l’on puisse obtenir des duretés distinctes suivant les faces où le test est effectué. L’exemple le plus connu est celui du disthène avec des duretés allant de 5 à 7.5 suivant les faces du cristal.
Il est tout à fait possible de trouver des minéraux où coexistent deux types de liaisons : des liaisons à caractère plutôt ionique et des liaison à caractère plutôt covalent. C’est le cas de nombreux silicates comme la forstérite de formule Mg₂SiO₄, qui comprend des liaisons ioniques magnésium/oxygène et des liaisons covalentes silicium/oxygène. Ce silicate doit notamment sa dureté à la présence de ces tétraèdres de silicium présentant des liaisons covalentes.
Les liaisons ioniques et covalentes ne sont pas les seules à expliquer la cohésion des solides cristallisés. Il existe en effet les liaisons dites « Hydrogènes » qui expliquent la cohésion de la glace, mais aussi les liaisons dites de « Van der Walls » qui expliquent une partie de la cohésion du graphite, l’autre étant expliquée par des liaisons covalentes carbone/carbone. Les liaisons Hydrogènes et les liaisons de Van der Walls sont qualifiées de liaisons faibles, car l’énergie nécessaire pour les rompre est bien moins importante que l’énergie nécessaire à la rupture de liaisons ioniques ou covalentes. Il serait trop compliqué d’expliquer l’origine de ces liaisons, aussi cet aspect ne sera pas abordé.
Pour terminer notre discussion autour de la cohésion des structures cristallines et de la dureté, il convient d’étudier le cas des micas. Ces minéraux sont des phylosilicates monocliniques, constitués d’empilement de feuillets. Pour la phlogopite de formule K(Mg,Fe²⁺)₃(Al,Fe³⁺)Si₃O₁₀(OH,F)₂ on note, dans les feuillets, la présence de liaisons très ioniques potassium/oxygène et magnésium/oxygène, puis de liaisons ionocovalentes fer/oxygène et enfin des liaisons très covalentes silicium/oxygène et aluminium/oxygène. Entre les feuillets, des liaisons Hydrogènes et de Van der Walls assurent la cohésion de l’édifice cristallin. Cette description simpliste suffit à expliquer l’existence d’un clivage basal parfait pour les micas. Les liaisons entre feuillets sont très faibles, un cristal peut être alors "découpé" avec l'ongle.

Lien entre densité, dureté et indice de réfraction

Quand on observe l’indice de réfraction des minéraux, on constante que la plupart des minéraux denses, ont un indice de réfraction important. On pourrait alors être tenté de croire que la densité et l’indice de réfraction sont des grandeurs liées. Il convient d’étudier ce phénomène avec rigueur. Le tableau qui suit, présente la densité, l’indice de réfraction et la dureté de divers carbonates isomorphes.

On remarque que le passage de l'aragonite à la whitérite ne modifie pas les indices de réfraction, cependant il y a une légère diminution de la dureté que l'on peut attribuer à une augmentation de la ionicité de la liaison alcalino-terreux-oxygène. En effet les liaisons calcium oxygène sont moins ioniques que les liaisons strontium oxygène, elles-mêmes moins ioniques que les liaisons baryum-oxygène. Ainsi on montre bien que la dureté n'est pas reliée à la densité.
Ces trois carbonates d'alcalino-terreux étant très ioniques et donc peu sujets à la déformation du nuage électronique, c'est pour cela que les indices de réfraction ne présentent pas d’évolution. Il en est tout autrement des propriétés de la cérusite, très dense (à cause du plomb) et présentant un fort indice. Cela est dû au fait que le plomb est « gros », le nuage électronique est donc très étendu d'où une grande sensibilité au champ électrique, ce qui se traduit par une permittivité électrique forte et donc un plus grand indice. La dureté de la cérusite est pourtant équivalente à celle des trois autres carbonates précités. Ainsi pour des minéraux de compositions chimiques distinctes il n’y a pas de réel lien entre la dureté, la densité et l’indice de réfraction.

Nature de la liaison chimique et indice de réfraction

Nous avons vu que la donnée pertinente concernant l’indice de réfraction est la polarisabilité des atomes. Cependant maintenant que nous avons introduit le concept de liaison chimique, il convient d’en regarder les effets sur l’indice de réfraction. Le tableau ci-dessous présente l’indice de réfraction, la densité et la dureté de divers minéraux classés par ionicité de liaison croissante.

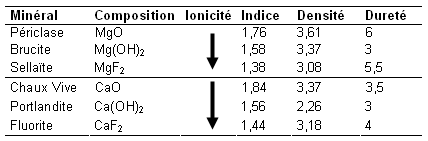
Pour les oxydes, hydroxydes et fluorures de magnésium on observe que l’indice de réfraction augmente avec la densité. Cependant ce phénomène n’est pas observé pour les oxydes, hydroxydes et fluorure de calcium. Le cas du magnésium est donc un cas particulier respectant la loi de Gladstone-Dale pour des compositions chimiques distinctes. Néanmoins il y a un phénomène plus marquant car commun au deux familles d’exemples : l’indice de réfraction diminue systématiquement quand la ionicité de la liaison augmente. L’explication est encore au niveau de la polarisabilité qui cette fois n’est pas atomique, mais se situe au niveau de la liaison chimique. Dans une liaison covalente, comme nous l’avons déjà dit, l’électron est partagé entre deux atomes. Cela peut se comparer aux orbitales atomiques diffuses des gros atomes. Ainsi l’électron sera plus sensible au champ électrique dans une liaison covalente que dans une liaison ionique où il sera bloqué à proximité des anions.

Dureté – Indice de réfraction : un lien finalement ?

Notre première approche de l’indice de réfraction montre qu’il dépend de la polarisabilité des atomes. Notre dernier axe d’étude concernant l’effet de la liaison chimique sur l’indice de réfraction montre que la ionocovalence de liaison a aussi son importance. Dans le cas des polymorphes de la silice, l’indice de réfraction évolue alors que la composition reste la même. Dans la mesure où nous avons étudié les liaisons atomiques et introduit le concept de polarisation nous pouvons apporter une réponse à ce problème. Le tableau ci-dessous donne la densité, l’indice de réfraction et la dureté en fonction des polymorphes de SiO₂.

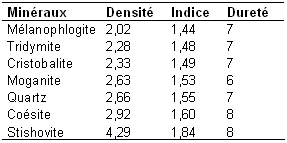
Sur le précédent tableau, on peut observer que parallèlement à l’augmentation de la densité, il y a une augmentation de la dureté des polymorphes de la silice, la seule exception étant observée pour la moganite. La coésite et le stishovite sont des minéraux stables sous forte pression. Quand la pression augmente, il y a contraction de la longueur des liaisons entre atome, ce qui explique l’augmentation importante de la densité pour la coésite mais surtout la stishovite. Or si la liaison devient plus courte, l’électron sera plus facilement délocalisé : la covalence de la liaison augmente et donc la dureté augmente également. Quand un électron est délocalisé sur une liaison, on se retrouve dans le cas équivalent d’un «  gros » atome avec des électrons loin du noyau et donc plus sensibles au champ électrique. Ainsi il y a augmentation de la polarisabilité et donc de l’indice de réfraction. Les liaisons devenant plus covalentes, il s’en suit une augmentation de la dureté.

Pour finir

Quand on compare deux minéraux de compositions chimiques distinctes, il n’y a pas de lien entre la dureté, la densité et l’indice de réfraction. Le paramètre pertinent est la polarisabilité des atomes en présence et le type de liaison chimique. Pour des polymorphes on peut trouver un lien entre dureté, densité et indice de réfraction. Quand la densité augmente, l’indice de réfraction fait de même, c’est la loi de Glastone-Dale. De même la dureté peut augmenter, ces deux effets étant dus à une augmentation de la covalence des liaisons quand celles-ci raccourcissent.

---

Voir aussi Les classifications en minéralogie

---

Retour à Lexique des termes employés en minéralogie

---

Retour au Portail Minéralogie